|
- Profº Sérgio Luiz
- EXPERIÊNCIAS
- CONTAS E TESTES COM AS 4 OPERAÇÕES
- ANÁLISE COMBINATÓRIA
- EXPRESSÃO NUMÉRICA
- EQUAÇÃO DO 1° GRAU
- EQUAÇÃO DO 2° GRAU
- EQUAÇÃOEXPONENCIAL
- ESTATÍSTICA
- EXPRESSÃO ALGÉBRICA
- FRAÇÕES
- FUNÇÃO DO 1° GRAU
- FUNÇÃO DO 2° GRAU
- LOGARITMOS
- MÍNIMO MÚLTIPLO COMUM (M.M.C)
- MAXIMO DIVISOR COMUM (M.D.C)
- MATRIZ E DETERMINANTES
- MONÔMIOS
- NÚMEROS NATURAIS
- NÚMEROS INTEIROS
- NÚMEROS RACIONAIS
- NÚMEROS IRRACIONAIS
- NÚMEROS REAIS
- NÚMEROS COMPLEXOS
- P.A
- P.G
- POTÊNCIAS
- POLINÔMIOS
- PROBABILIDADES
- PORCENTAGEM
- PROPORÇÂO
- PIADINHAS
- PRODUTOS NOTÁVEIS
- RADICAIS
- RAIZ QUADRADA
- RAIZ INEXATAS
- RAZÂO
- REGRA DE 3 SIMPLES
- REGRA DE 3 COMPOSTA
- SISTEMA DE EQUAÇÂO DO 1° GRAU
- TRIGONOMETRIA
- PERÍMETRO
- ÁREA
- RACIOCÍNIO LÓGICO
- DEIXE SEU RECADO AQUI
- CONTATOS
| enquete | ||
|
|
1 |
ANÁLISE COMBINATÓRIA
ANÁLISE COMBINATÓRIA
É importante observar que duas combinações são diferentes quando possuem elementos distintos, não importando a ordem em que os elementos são colocados.
“Combinação simples de n elementos tomados p a p ( ) são subconjuntos com exatamente p elementos que se podem formar com os n elementos dados”.
(1,2) (1,3) (1,4) (1,5) (2,3) (2,4) (2,5) (3,4) (3,5) (4,5)
Porque (1,2) ≠ (2,1) ; (1,3) ≠ (3,1) , etc.
Então, utilizando a fórmula geral para arranjos simples. Onde
Observe que trabalhamos com 2 elementos tomados p a p, do conjunto com o total de n=5 elementos. Ou seja, fizemos arranjos de2 a 2 com os 5 números do conjunto A.
, porque {1,2}={2,1} ; {1,3} = {3,1} , etc.
E o número de subconjuntos será:
Quer-se agrupar 3 elementos, dentre os 6 existentes.
Perceba que a ordem em que os elementos aparecerão não será importante, uma vez que, ao resolver a 1ª , a 2ª e a 3ª questão é o mesmo que resolver a 2ª , a 3º e a 1ª, portanto é um problema de combinação.
Logo, um aluno pode escolher suas 3 questões de 20 maneiras diferentes.
Observe que, se quiséssemos apenas fazer os arranjos destes elementos3 a 3, teríamos:
Faça você os arranjos, e depois verifique como foi feito nos exemplos anteriores, que esta afirmação é verdadeira.
Se fosse calculado o número de arranjos destas camisetas tomadas4 a 4, teríamos 3024 arranjos.
Preste atenção nesta próxima propriedade das combinações.
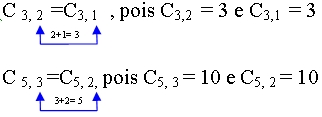
5º - No jogo de truco, cada jogador recebe 3 cartas de um baralho de 40 cartas(são excluídas as cartas 8, 9 , 10).
Portanto, cada jogador pode receber suas 3 cartas de 9880 maneiras diferentes.
DEFINIÇÃO
Combinação simples.
Denominamos combinações simples de n elementos distintos tomados p a p aos subconjuntos formados por p elementos distintos escolhidos entre os n elementos dados.
É importante observar que duas combinações são diferentes quando possuem elementos distintos, não importando a ordem em que os elementos são colocados.
Representando por Cn,p o número total de combinações de n elementos tomados p a p , temos a seguinte fórmula:
“Combinação simples de n elementos tomados p a p ( ) são subconjuntos com exatamente p elementos que se podem formar com os n elementos dados”.
Vamos relembrar alguns conceitos de arranjos.
Vamos passear um pouco por arranjos, e depois vamos seguir no mesmo exemplo trabalhando com combinação.
Vejamos um exemplo clássico.
1) Vamos considerar o conjunto A = {1,2,3,4,5}
Agora vamos formar todos os arranjos possíveis de 2 elementos distintos do conjunto A.
(1,2) (1,3) (1,4) (1,5) (2,3) (2,4) (2,5) (3,4) (3,5) (4,5)
(2,1) (3,1) (4,1) (5,1) (3,2) (4,2) (5,2) (4,3) (5,3) (5,4)
Porque (1,2) ≠ (2,1) ; (1,3) ≠ (3,1) , etc.
Note que usamos ( ) para denotar arranjos, pois são pares ordenados, o que implica em elementos distintos em cada agrupamento.
A simples mudança de ordem gera um novo par ordenado.
Então, utilizando a fórmula geral para arranjos simples. Onde
n= 5 (número total de elementos do conjunto A)
p= 2 (número de elementos tomados p a p – tomamos 2 elementos de cada vez para fazer os agrupamentos)
Observe que trabalhamos com 2 elementos tomados p a p, do conjunto com o total de n=5 elementos. Ou seja, fizemos arranjos de
Mas, e se quisermos saber, quantos subconjuntos de 2 elementos, podem ser formados por estes arranjos. Como proceder? Agora a conversa muda um pouco! Vamos ver como fica.
Os subconjuntos de 2 elementos que podemos formar são:
{1,2}, {1,3}, {1,4} ,{1,5} ,{2,3} ,{2,4} ,{2,5} ,{3,4}, {3,5}, {4,5}
Desta forma temos:
, porque {1,2}={2,1} ; {1,3} = {3,1} , etc.Note que usamos {} para denotar combinações, pois são subconjuntos, e a ordem dos elementos num subconjunto não se altera.
E com 3 elementos como fica? O número de arranjos será:
Temos: 
E o número de subconjuntos será:
Já deu para perceber que:
Vamos ver agora alguns exemplos mais elaborados.
EXERCÍCIOS RESOLVIDOS
1) Uma prova consta de 6 questões, das quais o aluno deve resolver 3. De quantas formas ele poderá escolher as 3 questões?
Quer-se agrupar 3 elementos, dentre os 6 existentes.
Perceba que a ordem em que os elementos aparecerão não será importante, uma vez que, ao resolver a 1ª , a 2ª e a 3ª questão é o mesmo que resolver a 2ª , a 3º e a 1ª, portanto é um problema de combinação.
Logo, um aluno pode escolher suas 3 questões de 20 maneiras diferentes.
Observe que, se quiséssemos apenas fazer os arranjos destes elementos
Faça você os arranjos, e depois verifique como foi feito nos exemplos anteriores, que esta afirmação é verdadeira.
2) De quantos modos distintos Amiroaldo pode escolher quatro entre as nove camisetas regata que possui para levar em uma viagem para Mosqueiro.
Suponha que Amiroaldo escolha as camisas 1, 2, 3 e 4.
Amiroaldo escolhendo as camisas:
Veja que (1, 2, 3, 4) = (1, 3, 4, 2), pois não importa em que ordem Amiroaldo escolhe as camisas que vai levar, o importante é que as camisas escolhidas são as mesmas na primeira e na segunda situação. Problemas como esses são resolvidos com a idéia de Combinação simples.
Existem 126 maneiras diferentes para Amiroaldo escolher 4 camisetas das 9 que possui.
Se fosse calculado o número de arranjos destas camisetas tomadas
3) Ane, Elisa, Rosana, Felipe e Gustavo formam uma equipe. Dois deles precisam representar a equipe em uma apresentação. Quais e quantas são as possibilidades?
Representamos cada pessoa por uma letra
A: Ane;
E: Elisa;
R: Rosana;
F: Felipe;
G: Gustavo
.
Precisamos determinar todos os subconjuntos de 2 elementos do conjunto de 5 elementos {A,E,R,F,G}. A ordem em que os elementos aparecem nos subconjuntos não importa, pois Ane-Elisa, por exemplo, é a mesma dupla que Elisa-Ane.Então, os subconjuntos de 2 elementos são?
{A,E},{A,R},{A,F},{A,G},{E,R}{E,F},{E,G},{R,F},{R,G}{F,G}.
Chamamos estes subconjuntos de combinação simples de 5 elementos tomados com 2 a 2. Escrevemos C5,2 .
Onde C5, 2 representa a fórmula das combinações simples:
Substituindo na fórmula
Preste atenção nesta próxima propriedade das combinações.
Propriedade importante das combinações:
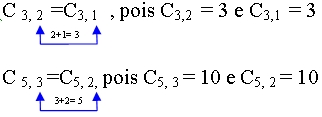
De modo geral temos que:
Cn, p = Cn, n-p
Exercícios resolvidos – Número binomial de ordem n e classe p.
1º - Vamos calcular o valor de:
5º - No jogo de truco, cada jogador recebe 3 cartas de um baralho de 40 cartas(são excluídas as cartas 8, 9 , 10).
De quantas maneiras diferentes um jogador pode receber suas 3 cartas
As 3 cartas diferem entre si pela natureza delas, e não pela ordem. Como a ordem não importa, calculamos?
Portanto, cada jogador pode receber suas 3 cartas de 9880 maneiras diferentes.