
ESTATÍSTICA
DEFINIÇÕES E CONCEITOS BÁSICOS
A Estatídstica pode ser definida como um conjunto de métodos e processos quantitativos utilizada para estudar, mensurar e rerpresentar os fenômenos coletivos.
A Estatística teve grande desenvolvimento a partir do século XVII, por meio ddas inveastigações de BERNOULLI, FERMAT, PASCAL, LAPLACE, GAUSS, GALTON, PEARSON, FISHER, POISSON, KOLMOGOROV e outros que conceberam suas características essenciais. Ela não alcançou ainda um estado definitivo. Continua a progredir na ação direta do desejo de investigação dos fenômenos coletivos.
Mantém com a Matemática uma relação de dependência, com as outras Ciências mantém uma relação de complemento, sendo utilizada como instrumento de pesquisa.
Essa relação de complemento é o meio que a Estatística, utilizando seus MÉTODOS ESTATÍSTICOS, serve como instrumento auxiliar na tomada de decisões, nas Áreas Tecnológicas, Ciências Exatas, Ciências HUmanas, Ciências da Saúde e outras.
Para Levine (2008), a Estatística transforma os dados em informações úteis para a tomada de decisões. Necessita de cálculos complexos que podem ser práticos se realizados com o auxílio de computadores, pois normalmente se lida com grande volume de dados. Por este motivo, é necessário, também, conhecer progrmamas de computadores que realizam cálculos e análises estatísticas.
Nesse sentido., estatísticas são fatos numéricos que são coletados sistematicamente, depois são ordenados e estudados (SMAILES, 2006).
A Estatística é considerada como Ciência no sentido do estudo de uma população.
A Estatística tem como OBJETIVO o estudo dos fenômenos coletivos.
Objetivando o estudo quantitativo e qualitativo dos dados (ou informações), obtidos nos vários campos da atividade científica, a Estatística manipula dois conjuntos de dados fundamentais: a "população" e a "amostra".
População ou Universo
É o conjunto de todos os seres, objetos ou informações que interessam ao estudo de um fenômeno coletivo segundo algumas características.
Na maioria das vezes, não é conveniente, ou mesmo possível realizar o levantamento dos dados referentes a todos os elementos de uma população. Portanto, analisamos parte da população, isto é amostramos.
Amostra
É uma parcela ou subconjunto da população que é selecionada para se analisar. Duas considerações devem ser feitas sobre o estudo amostral dos fenômenos. Uma diz respeito aos cuidados que se deve tomar para assegurar que a amostra seja representativa da população. Para atender a essa exigência, deve-se selecionar os elementos de forma aleatória, de modo que todo e qualquer elemento da população tenha a mesma chance de participar da amostra. A outra exigência diz respeito à precisão dos dados coletados, buscando minimizar os erros que poderiam induzir a conclusões equivocadas. O número de elementos de uma amostra é chamado o tamanho da amostra.

Parâmetro
É toda medida numérica utilizada para descrever características de uma polulação.
Estimativa
É toda medida numérica utilizada para descrever características de uma amostra.
Por exemplo: no fenômeno coletivo eleição para prefeito do município de Bauru, a população é o conjunto de todos os eleitores habilitados na respectiva cidade. Um parâmetro é a proporção de votos do candidato A. Uma amostra pode ser um grupo de 1.000 eleitores selecionados em todo o município. Um estimador é a proporção de votos de um candidato obtida na amostra. O valor resultante do estimador, a proporção amostral, é a estimativa.
Em aplicações efetivas, onde aplica-se o processo de amostragem, o número de elementos componentes de uma amostra é, geralmente, bastante reduzido em relação ao número de elementos componentes da população.

DADOS e VARIÁVEIS ESTATÍSTICAS
Dados
Normalmente, no trabalho estatístico o pesquisador se vê obrigado a lidar com grande quantidade de valores numéricos resultantes de um censo ou de uma amostragem. Estes valores numéricos são chamados dados estatísticos.
Os dados estatísticos resultantes da coleta direta da fonte, por meio de contagem ou medida, são chamadosdados absolutos.
Dados relativos são o resultado de comparações por razões que se estabelecem entre dados absolutos e têm por finalidade realçar ou facilitar as comparações entre quantidades. São as percentagens, índices, coeficientes etaxas.
Variável
É toda característica de um item ou de un indivíduo.
As informações ou dados característicos dos fenômenos ou populações são denominados variáveis estatísticas ou simplesmente variáveis. Conforme suas características particulares, podem ser classificadas como: Quantitativase Qualitativas.
QUANTITATIVAS - São aquelas que podem ser expressas em termos numéricos.
Em geral são as resultantes de medições, enumerações ou contagens. São subdivididas em contínuas ediscretas.
Contínuas - são aquelas que podem assumir qualquer valor num certo intervalo de medida, podendo ser associados ao conjunto dos números reais, ou seja, seus valores possíveis formam um conjunto não enumerável. Entre outras, enquadram-se nesta categoria as medidas de tempo, comprimento, espessura, área, volume, peso e velocidade.
Discretas (ou descontínuas) - quando só podem assumir determinados valores num certo intervalo, podendo ser associadas ao conjunto dos números inteiros, ou seja, seus possíveis valores formam um conjunto finito ou enumerável. Em geral, representam números inteiros resultantes do processo de contagem, como o número de alunos por sala, de créditos por disciplinas, de pacientes atendidos diariamente num hospital, etc.
De modo geral, as medições dão origem as variáveis contínuas e as contagens ou enumerações, as variáveis discretas. Designamos estas variáveis por letras latinas, em geral, as últimas: X, Y, Z.
QUALITATIVAS - Nem sempre os elementos de uma população são exclusivamente contáveis. Muitas vezes, eles podem ser qualificados também segundo algumas de suas características típicas. Nesses casos, as variáveis podem ser agrupadas em nominais ou ordinais( por postos ).
Nominais - quando puderem ser reunidas em categorias ou espécies com idênticos atributos. Aqui se incluem os agrupamentos por sexo, área de estudo, desempenho, cor, raça, nacionalidade e religião.
Ordinais - quando os elementos forem reunidos segundo a ordem em que aparecem dispostos numa lista ou rol. São típicos desta forma de agrupamento, as listas classificatórias de concursos e as tabelas de campeonatos.
Em geral, uma mesma população pode ser caracterizada por mais de um tipo de variável. Assim os inscritos num vestibular, por exemplo, podem ser contados, medidos ou pesados, podem ser agrupados segundo o sexo ou área de estudo e podem ainda ser classificados segundo as notas obtidas nas provas prestadas.

PROCESSOS ESTATÍSTICOS DE ABORDAGEM
Quando solicitados a estudar um fenômeno coletivo podemos optar entre os seguintes
processos estatísticos:
CENSO - avaliação direta de um parâmetro, utilizando-se todos os componentes da população.
Propriedades Principais do Censo: Admite erro processual zero e tem confiabilidade 100% - É caro.
É lento - É quase sempre desatualizado - Nem sempre é viável.
AMOSTRAGEM (Inferência) - avaliação indireta de um parâmetro, com base em
um estimador através do cálculo das probabilidades.
Propriedades Principais da Estimação: Admite erro processual positivo e tem confiabilidade menor que 100% - É barata – É rápida - É atualizada - É sempre viável.
No sentido de disciplina, a Estatística ensina métodos racionais para a obtenção de informações a respeito de um fenômeno coletivo, além de obter conclusões válidas para o fenômeno e também permitir tomada de decisões, através de alguma(s) característica(s) de valores numéricos observados.
Desta forma, a Estatística pode ser dividida em duas grandes áreas: Descritiva e Inferencial.
ESTATÍSTICA DESCRITIVA
É a parte da Estatística que tem por objetivo descrever os dados observados. São atribuições da Estatística Descritiva:
a) A organização dos dados.
b) A redução dos dados.
c) A representação dos dados.
d) A obtenção de algumas informações que auxiliam a descrição do fenômeno observado.
A organização dos dados consiste na ordenação e crítica quanto à correção dos valores observados, falhas humanas, omissões, abandono de dados duvidosos, etc.
Redução dos dados - O entendimento e compreensão de grande quantidade de dados através de simples leitura de seus valores individuais é uma tarefa extremamente árdua e difícil mesmo para o mais experimentado pesquisador, portanto deveremos tabular os dados.
A representação dos dados - Os dados estatísticos podem ser mais facilmente compreendidos quando apresentados através de uma representação gráfica, a qual permite uma visualização instantânea de todos os dados. Os gráficos quando bem representativos, tornam-se importantes instrumentos de trabalho.
A obtenção de algumas informações que sumarizam os dados, facilitando a descrição dos fenômenos observados. Isto encerra as atribuições da Estatística Descritiva.
ESTATÍSTICA INFERENCIAL (ou Indutiva)
É a parte da Estatística que tem por objetivo obter e generalizar conclusões para a população a partir de uma amostra.
Complementando o processamento estatístico, no caso de uma estimação, a Estatística Indutiva estuda os parâmetros a partir do uso de estimadores usando o cálculo das probabilidades, elemento este que viabiliza a inferência estatística.
Em resumo, um estudo estatístico completo que recorra às técnicas de Estatística Inferencial irá envolver também, direta ou indiretamente, tópicos de Estatística Descritiva, Cálculo das Probabilidades e Amostragem. Logo, para se desenvolver um curso completo e razoável de Estatística, todos esses assuntos devem ser abordados.


PROJETO GERAL DE PESQUISA
De acordo com Smailes (2006), segue uma lista de verificação das principais etapas do projeto de uma pesquisa.

Planejamento:
- Defina as metas da pesquisa.
- Defina a população.
- Identifique cada membro da população.
- Identifique o esquema de amostragem (como escolher a amostra e que tamanho ela deve ter).
- Decida que método de coleta de dados utilizar (questionário postal,entrevista etc.).
- Projete um questionário (igualmente apropriado para entrevistas pessoais e observação).
- Selecione e treine qualquer pessoa envolvida no processo de coleta de dados.
Trabalho de campo:
- Selecione a amostra.
- Colete os dados.
- Vá atrás de qualquer resposta que falte sempre que possível.
- Ordene e codifique as informações (principalmente se um computador for utilizado para a análise).
Análise e interpretação:
- Filtre os dados buscando erros de registro e valores extremos.
- Execute qualquer cálculo estatístico.
- Identifique e observe qualquer causa possível de erro e/ou vício.
Publicação:
Geralmente em duas seções:
- Resultados escritos e conclusões.
- Seção estatística detalhada que inclui:
- Detalhes dos questionários utilizados;
- Detalhes da amostragem;
- Teoria estatística por trás da pesquisa;
- Resumo dos dados coletados.

Tabelas
Os dados numéricos, após coletados são colocados em série e apresentados em tabelas ou quadros.
Ao se estudar uma variável, seja quantitativa ou qualitativa, o pesquisador procura conhecer sua distribuição por meio de suas possíveis realizações. As tabelas de distribuição de frequências auxiliam a resumir os dados de forma a se ter uma boa idéia global dos valores encontrados.
Um dos objetivos da Estatística é sintetizar os valores que uma ou mais variáveis podem assumir, para que tenhamos uma visão global da variação dessas variáveis (CRESPO, 2009).
Tabela
É um quadro que resume um conjunto de observações. É uma disposição escrita que se obtém referindo-se a uma coleção de dados numéricos a uma determinada ordem de classificação.
De um modo geral tem-se a destacar em uma tabela:
Elementos essenciais:
- Indicação que precede a tabela e que contém a designação do fato observado, o local e a época em foi registrado.
- Título:
- : Parte superior da tabela que especifica o conteúdo das colunas.
- Cabeçalho
- Coluna Indicadora: Parte da tabela que especifica o conteúdo das linhas.
- : Conjunto de colunas e linhas que contém as informações sobre a variável em estudo.
- Corpo da tabela
- Linhas: retas imaginárias que facilitam a leitura, no sentido horizontal, de dados que se inscrevem nos seus cruzamentos com as colunas.
- Casa ou Célula: espaço destinado a um só número.
Elementos complementares:
- : Indicação da entidade responsável pelo fornecimento dos dados ou pela sua elaboração.
- Fonte
- : Informações de natureza geral destinadas a conceituar ou esclarecer o conteúdo das tabelas ou a indicar a metodologia adotada no levantamento ou na elaboração dos dados.
- Notas
- Chamadas: Informações de natureza específica sobre determinada parte da tabela, destinada a conceituar ou a esclarecer dados.
De acordo com as normas da Fundação IBGE, nas casas ou células devemos colocar:
- Um traço horizontal (-) quando o valor é zero;
- Três pontos (...) quando não temos os dados;
- Um ponto de interrogação (?) quando temos dúvida quando à exatidão de determinado valor;
- Zero (0) quando o valor é muito pequeno para ser expresso pela unidade utilizada.

Séries estatísticas
De acordo com Crespo (2009), série estatística é toda tabela que apresenta a distribuição de um conjunto de dados estatísticos em função de tempo, do local ou da espécie. Em uma série estatística observamos a existência de três elementos ou fatores: o tempo, o espaço e a espécie. São classificadas em histórica, geográfica e específica.
- Séries históricas: descrevem os valores da variável, em determinado local, discriminados segundo intervalos de tempo variáveis.
- Séries Geográficas: descrevem os valores da variável, em determinado instante, discriminados segundo regiões.
- Séries específicas: descrevem os valores da variável, em determinado tempo e local, discriminados segundo especificações ou categorias.
Muitas vezes é necessário apresentar, em uma única tabela, a variação de valores de mais de uma variável, isto é, fazer uma composição de duas ou mais séries.

Distribuições de Frequências
De acordo com Fonseca (2011), trata-se do tipo de tabela mais importante para a Estatística Descritiva.É uma disposição de dados, de acordo com o tamanho ou a magnitude
dos mesmos.
dos mesmos.
As distribuições de frequências apresentam:
• A frequência (quantidade) que ocorre determinado resultado;
• Simetria / assimetria;
• Onde se concentram os valores;
• Dispersão;
• Valores discrepantes;
• Estratificação (diferentes subgrupos de dados).
• Simetria / assimetria;
• Onde se concentram os valores;
• Dispersão;
• Valores discrepantes;
• Estratificação (diferentes subgrupos de dados).
A tabela de frequências mostra a relação entre a variável e a quantidade de vezes que cada valor se repete. Essa tabela pode ser representada por valor (único) ou por intervalos (classes).
Alguns conveitos funfamentais:
Dados brutos: é o conjundo dos valores númericos coletados na pesquisa. Estes valores podem ser digitados em planilha e criticados buscando identificar possíveis erros, respostas omitidas e valores muito discrepantes.
Rol: é a ordenação dos dados brutos de forma crescente ou decrescente.
Frequência absoluta (fi): é o número de vezes que um elemento aparece na amostra, ou o número de elementos pertencentes a um intervalo ou classe.
Distribuição de frequências por valores
Utilizada para variáveis qualitativas ou quantitativas discretas.
É construída considerando-se todos os diferentes valores ou categorias, levando em consideração suas respectivas repetições. Ou seja, é obtida pela contagem de cada valor encontrado.

Distriuição de frequências por intervalos ou classes
Utilizadas para variáveis quantitativas.
Se constrói classes de valores, quando a variabilidade dos dados é grande, levando em consideração o número de valores que pertencem a cada classe. A construção de tabelas de frequências para variáveis contínuas necessita de certos cuidados.
Ao se agrupar os valores da variável em classes, ganha-se em simplicidade, mas perde-se em detalhes e precisão. O que se pretende com a construção dessa nova tabela é realçar o que há de essencial nos dados e, também, tornar possível o uso de técnicas analíticas para sua total descrição, até porque a Estatística tem por finalidade específica analisar o conjunto de valores, desinteressando-se por casos isolados.

Orientações básicas para a elaboração de uma tabela de distribuição de frequência por intervalos ou classes:
- Efetua-se um (ordenação crescente ou decrescente de grandeza) nos dados brutos.rol estístico
- Determina-se a dos dados: amplitude total

Onde:
Xmáx = maior valor observado e
Xmín = menor valor observado.
- Escolhe-se convenientemente o número de classes (número inteiro), 5 ≤ ≤ 15, onde podemos tomar:K K

Onde:
k = número de classes
n = quantidade total de dados (tamanho da amostra)
ou a fórmula de Sturges

Nos dois casos, deve-se arredondar para cima o valor encontrado.
- Se possível constrói-se classes de mesma amplitude , tomando:(h)

O valor encontrado também é arredondado para cima.
Alguns conceitos essenciais:
Limites das classes: Li (limite inferior) Ls (limite superior)
Li |-------- Ls - compreende todos os valores maiores ou iguais a Li e menores que Ls, ou seja o valor do limite superior não é contado no intervalo.
Amplitude da classe (hi): é a diferença entre o limite superior e o limite inferior da classe.
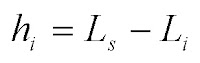
Ponto médio da classe (xi): é a média entre o limite superior e o limite inferior da classe.

Frequência relativa (fri): é o valor da razão de cada frequência absoluta (fi) com a frequência total (somatório de fi).

Frequência relativa percentual (fri%): é a frequência relativa em forma de percentagem.
Alguns conceitos essenciais:
Limites das classes: Li (limite inferior) Ls (limite superior)
Li |-------- Ls - compreende todos os valores maiores ou iguais a Li e menores que Ls, ou seja o valor do limite superior não é contado no intervalo.
Amplitude da classe (hi): é a diferença entre o limite superior e o limite inferior da classe.
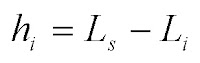
Ponto médio da classe (xi): é a média entre o limite superior e o limite inferior da classe.

Frequência relativa (fri): é o valor da razão de cada frequência absoluta (fi) com a frequência total (somatório de fi).

Frequência relativa percentual (fri%): é a frequência relativa em forma de percentagem.
Frequência acumulada (Fi): é obtida somando (acumulando) os valores da frequência absoluta. A primeira frequência acumulada é igual ao valor da primeira frequência absoluta. As demais obtém-se acumulando as frequências absolutas.
Frequência acululada percentual (Fri%): é obtida somando (acumulando) os valores da frequência relativa percentual. A primeira frequência acumulada é igual ao valor da primeira frequência relativa percentual. As demais obtém-se acumulando as frequências relativas percentuais.
Tabela completa de frequências

Gráficos
Representação gráfica de dados
Além de utilizar tabelas para resumir um conjunto de dados, os gráficos fornecem um impacto visual alternativo. Ográfico estatístico é uma forma de apresentação dos dados estatísticos, cujo objetivo é o de produzir, no investigador ou no público em geral, uma impressão mais rápida e viva do fenômeno em estudo, já que os gráficos são mais rápidos de serem compreendidos que as tabelas.
A representação gráfica objetiva a representação dos resultados obtidos, de forma a se tomar conclusões sobre a evolução do fenômeno ou como os valores das séries se relacionam.
Existem várias formas para se representar graficamente os dados. O investigador deve escolher o gráfico mais adequado. Mas devem-se considerar alguns requisitos fundamentais: simplicidade, clareza e veracidade.
Ao construir qualquer tipo de gráfico, é importante observar:
- Titulo adequado;
- Eixos rotulados; e
- Escala sensata utilizada.
Um gráfico deve fazer sentido e ser facilmente compreendido, mesmo se nenhum dado acompanhá-lo.

Gráfico de Colunas
Normalmente, é o tipo de gráfico mais utilizado. Cada categoria é representada por uma barra retangular distinta, sendo a frequência indicada pelo comprimento/altura da barra.
Não utilizado para dados contínuos e dados ordinais na forma de série temporal.
Gráfico de Barras
É semelhante ao gráfico de colunas, porém a representação das frequências são dispostas de forma horizontal.


Gráfico de Setores
Todo o conjunto de dados é representado por um círculo e cada categoria representada por uma parte (setor) do círculo.
Utilizado para representar proporções, quando se pretende comparar cada valor da série com o total.
Para sua construção, normalmente utiliza-se os dados da frequência percentual.
Não recomendado para grande número de categorias.

Gráfico de Linha
Este tipo de gráfico se utiliza da linha poligonal para representar a série estatística.
O gráfico em linha é uma aplicação do processo de representação das funções num sistema de coordenadas cartesianas.
Nesse sistema se utiliza duas retas perpendiculares; as retas são os eixos coordenados e o ponto de intersecção, a origem. O eixo horizontal é denominado eixo das abscissas (ou eixo dos x) e o vertical, eixo das ordenadas (ou o eixo dos y).
Ele simplesmente consiste na variável tempo plotada no eixo horizontal e na segunda variável plotada no eixo vertical.
Normalmente utilizado para representar dispersão série temporal.
O gráfico de dispersão é utilizado para verificar possíveis relações entre duas variáveis, enquanto que o gráfico de séries temporais utilizado para verificar os padrões de uma variável ao longo go tempo.
Histograma
O histograma é utilizado para fornecer o equivalente ao gráfico de barras para dados contínuos que foram agrupados em tabela de distribuição de frequência.
Cuidado ao falar de histograma, geralmente é um gráfico de barras que foi utilizado.
Existem duas diferenças principais:
- O eixo inferior possui uma escala contínua e os blocos são dispostos juntos;
- A área de cada bloco representa a frequência.
Ou seja, o histograma é semelhante ao gráfico de barras, mas nesse tipo de gráfico, não existem espaços em branco entre as colunas.

Polígono de Frequências
Um polígono de frequência é um gráfico que se realiza através da união dos pontos mais altos das colunas num histograma de frequência (que utiliza colunas verticais para mostrar as frequências).
Os polígonos de frequência para dados agrupados, por sua vez, constroem-se a partir da marca de classe que coincide com o ponto médio de cada coluna do histograma.

Polígono de Frequência Acumulada
Quando são representadas as frequências acumuladas de uma tabela de dados agrupados, obtém-se um histograma de frequências acumuladas, que permite dispor em diagrama o seu polígono correspondente.
O gráfico de frequência acumulada, ou ogiva, também é utilizado para dados contínuos.
O principal uso é para encontrar medidas como medianas e intervalos interquartis.

Medidas de Tendência Central
As medidas de tendência central recebem tal denominação pelo fato de os dados observados tenderem, em geral, a se agrupar em torno dos valores centrais.
Média Aritmética
Geralmente conhecida como média é a medida de tendência central mais comum. É a única medida na qual os valores desempenham igual papel. Serve como um ponto de equilíbrio em um conjunto de dados.
É calculada simplesmente somando-se todos os valores observados para uma variável em um conjunto de dados e dividindo-se o resultado pelo número total de itens no conjunto de dados.

Mediana
É o valor do meio de um conjunto de dados que tenha sido ordenado do menor para o maior.
Metade dos valores é menor ou igual à mediana e a outra metade dos valores é maior ou igual à mediana.
A mediana não é afetada por valores extremos, portanto ela pode ser utilizada quando estão presentes valores extremos.
Para calcular a posição da mediana utiliza-se a seguinte equação:

Calcula-se a mediana seguindo-se uma das seguintes regras:
Regra 1 – quantidade de dados ímpares: a mediana é o valor que está no meio da ordem de classificação.
Regra 2 – Se existir uma quantidade par de dados ordenados, a mediana corresponde à média dos dois valores que estão no meio na ordem de classificação.
Moda
A moda é o valor que aparece com mais frequência em um conjunto de dados. Do mesmo modo que a mediana, e diferentemente da média, não é afetada por valores extremos. Em um conjunto de dados pode existir várias modas ou não existir nenhuma moda.
Medidas Separatrizes
São números que dividem a sequência ordenada de dados em partes que contêm a mesma quantidade de elementos da série.
Desta forma, a mediana que divide a sequência ordenada em dois grupos, cada um deles contendo 50% dos valores da sequência, é também uma medida separatriz.
Além da mediana, as outras medidas separatrizes são: quartis, quintis, decis e percentis.
Quartis
Ao dividir a série ordenada em quatro partes, cada uma ficará com seus 25% de seus elementos.
Os elementos que separam estes grupos são chamados de quartis.
Assim, o primeiro quartil, que indicado por Q1, separa a sequência ordenada deixando 25% de seus valores à esquerda e 75% de seus valores à direita.
O segundo quartil, indicado por Q2, separa a sequência ordenada deixando 50% de seus valores à esquerda e 50% de seus valores à direita. O Q2 é a Mediana da série.
O terceiro quartil Q3 obedece a mesma regra dos anteriores.
Quintis
Ao dividir a série ordenada em cinco partes, cada uma ficará com seus 20% de seus elementos.
Os elementos que separam estes grupos são chamados de quintis.
Assim, o primeiro quintil, indicado por K1, separa a sequência ordenada deixando 20% de seus valores à esquerda e 80% de seus valores à direita.
De modo análogo são definidos os outros quintis.
Decis
Ao dividir a série ordenada em dez partes, cada uma ficará com seus 10% de seus elementos.
Os elementos que separam estes grupos são chamados de decis.
Assim, o primeiro decil, indicado por D1, separa a sequência ordenada deixando 10% de seus valores à esquerda e 90% de seus valores à direita.
De modo análogo são definidos os outros decis.
Percentis
Ao dividir a série ordenada em cem partes, cada uma ficará com 1% de seus elementos.
Os elementos que separam estes grupos são chamados de centis ou percentis.
Assim, o primeiro percentil, indicado por P1, separa a sequência ordenada deixando 1% de seus valores à esquerda e 99% de seus valores à direita.
De modo análogo são definidos os outros percentis.
Verifica-se que os quartis, quintis e decis são múltiplos dos percentis, então basta estabelecer a fórmula de cálculo de percentis. Todas as outras medidas podem ser identificadas como percentis. Ou seja:
|
Percentis
|
Quartis
|
Quintis
|
Decis
|
|
P10
|
|
|
D1
|
|
P20
|
|
K1
|
D2
|
|
P25
|
Q1
|
|
|
|
P30
|
|
|
D3
|
|
P40
|
|
K2
|
D4
|
|
P50
|
Q2
|
|
D5
|
|
P60
|
|
K3
|
D6
|
|
P70
|
|
|
D7
|
|
P75
|
Q3
|
|
|
|
P80
|
|
K4
|
D8
|
|
P90
|
|
|
D9
|
Cálculo da separatriz:
Identifica-se a medida que se pretende obter com o percentil correspondente, Pi.
Calcula-se i% de n para localizar a posição do percentil i no Rol, ou seja:

Em seguida, identifica-se o elemento que ocupa esta posição.
Note que se o elemento for um número inteiro, então o Pi procurado é um dos elementos da sequência ordenada.
Se não for um número inteiro, isto significa que Pi é um elemento intermediário entre os elementos que ocupam as posições aproximadas por falta ou por excesso do valor calculado. Neste caso, Pi é definido como sendo a média dos valores que ocupam estas posições aproximadas.








