Potenciação de Radicais
Observando as potencias, temos que:
De modo geral, para se elevar um radical a um dado expoente, basta elevar o radicando àquele expoente. Exemplos:
Divisão de Radicais
Segundo as propriedades dos radicais, temos que:De um modo geral, na divisão de radicais de mesmo índice, mantemos o índice e dividimos os radicais: Exemplos:
Se os radicais forem diferentes, devemos reduzi-los ao mesmo índice e depois efetue a operação. Exemplos:
Fonte: www.somatematica.com.br
Radiciação
A matéria de radiciação acaba ficando bem mais fácil se você já viu "Potenciação".Radiciação é o inverso da potenciação. Por exemplo, se elevarmos um número X à quinta potência e depois tirar a raiz quinta do resultado, voltamos ao número X.
Exemplos
Para acharmos a raiz cúbica de oito (), devemos nos perguntar qual o número que multiplicado por ele mesmo três vezes resulta 8, ou seja, qual o número que elevado na potência 3 resulta 8?. A resposta é 2, pois 23=2·2·2=8Nomenclatura:


Vamos agora ver alguma propriedades fundamentais de radiciação:
an/n
e a fração n/n vale 1, então:
an/n = a1= a
Estas são as principais propriedades de Radiciação. Agora vamos ver as propriedades operatórias, ou seja, como fazer operações com raizes (multiplicação, divisão...).
PROPRIEDADES OPERATÓRIAS
Agora vamos dar uma visão mais genérica, visto que as propriedades irão se repetir pois são idênticas às de potênciação:Novamente se transformarmos a raiz em potência, teremos:

Agora o que devemos fazer é voltar de potência para raiz:
Fonte: www.cursinho.hpg.ig.com.br
RADICIAÇÃO
A radiciação é a operação matemática oposta à potenciação (ou exponenciação).A notação matemática da radiciação é:
Onde
A aplicação prática da radiciação se dá pela equivalência:
Ou, de forma mais didática:
Propriedades da radiciação

Fonte: pt.wikipedia.org
Radiciação
A radiciação é a operação inversa da potenciação e, por isso, ela se define através da seguinte relação:
a é um número real chamado radicando;
n é um número natural diferente de zero, chamado índice.
O resultado da operação é um número real b, chamado raiz.
Potência de expoente racional
Como decorrência dessa última igualdade, são válidas, também para a radiciação, todas as propriedades operatórias citadas para a potenciação
Fonte: www.ucs.br
Propriedades dos RadicaisRADICAIS 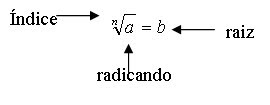 A raiz de índice par de um número não-negativo é um número real não-negativo.
A raiz de um radical de índice ímpar tem o mesmo sinal do radicando. Potência com expoente fracionária: relacionando radiciação com potenciação. Se a é um número real positivo, m é um número inteiro e n é um número natural não-nulo, temos: Propriedades dos radicais 1ª propriedade: Para os radicais de índice n de uma potência com expoente também igual a n temos: 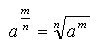 se n é um número natural ímpar, então: 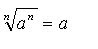 sendo a um número real; sendo a um número real;se n é um número natural par não-nulo, então:
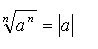 com a um número real. com a um número real.2ª propriedade: Dividindo-se o índice e o expoente do radicando por um mesmo número natural maior que zero, o valor do radical não se altera, ou seja: 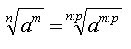 1. sendo a um número real positivo, m um número inteiro, n um número natural não-nulo e p divisor de m e n. 2. Essa propriedade permite simplificar certos radicais, isto é, transformá-lo em outros radicais mais simples e equivalentes aos radicais dados. 3ª propriedade:
O radical de índice natural não-nulo n de um produto , com a e b números reais positivos, é igual ao produto dos radicais de mesmo índice n dos fatores (a e b) do radicando, ou seja: 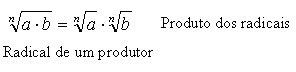 4ª propriedade: O radical de índice natural não-nulo n de um quociente , com a e b números reais positivos, é igual ao quociente dos radicais de mesmo índice n dos termos a e b do radicando, ou seja: 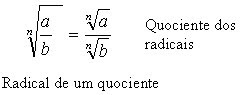 1. Essas propriedades permitem simplificar certos radicais, tirando fatores do radicando. 1. Essas propriedades permitem simplificar certos radicais, tirando fatores do radicando.2. Da mesmo forma que podemos tirar fatores do radicando, podemos fazer o inverso, ou seja, introduzir fatores externos no radicando. Veja os exemplos: Observações: Não se pode somar nem subtrair radicais diferentes. Imagine as raízes como letras. Letras iguais: podem ser somadas ou subtraídas, divididas ou multiplicadas. Letras diferentes se podem apenas ser divididas ou multiplicadas uma pelas outras:
Analogamente ao que acontece com os radicais: É impossível fazer: x + y ou x – y, mas é possível fazer: xy e x/y ou ainda x + x = 2x e x – x = 0. |







