FRAÇÃO
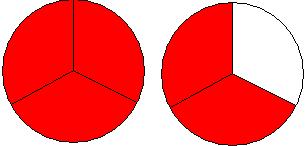
Fração é a representação da parte de um todo (de um ou mais inteiros), assim, podemos considerá-la como sendo mais uma representação de quantidade, ou seja, uma representação numérica, com ela podemos efetuar todas as operações como: adição, subtração, multiplicação, divisão, potenciação, radiciação.
Dessa forma, toda fração pode ser representada em uma reta numerada, por exemplo, 1/2 (um meio) significa que de um inteiro foi considerada apenas a sua metade, portanto, podemos dizer que em uma reta numerada a fração 1/2 estará entre os números inteiros 0 e 1.
Por ser uma forma diferente de representação numérica, a fração irá possui uma nomenclatura específica e poderá ser escrita em forma de porcentagem, números decimais (números com vírgula) e números mistos.
Assim, podemos concluir que o surgimento do número fracionário veio da necessidade de representar quantidades menores que inteiros, por exemplo, 1 bolo é um inteiro, mas se comermos um pedaço, qual seria a representação numérica que esse pedaço e o resto do bolo representaria? Foi a necessidade de criar uma representação numérica para as partes de um inteiro que proporcionou o surgimento dos números fracionários que iremos estudar nesta seção.
Adição e subtração de fração
As operações de adição e subtração com fração dependem unicamente do denominador, ou seja, dependem da quantidade de partes que um inteiro foi dividido. Podendo ser iguais ou diferentes, assim diferenciando a resolução.
Quando os denominadores forem iguais devemos somar ou diminuir as partes consideradas do inteiro (numeradores) e conservar as partes que o inteiro foi dividido (denominadores).
1/5 + 2/5 = 3/5, pois somamos os numeradores 1 + 2 e conservamos o denominador 5.
3/4 + 2/4 = 5/4, pois somamos os numeradores 3 + 2 e conservamos o denominador 4.
2/5 – 1/5 = 1/5, pois subtraímos os numeradores 2 -1 e conservamos o denominador 5.
Quando os denominadores forem diferentes é preciso torná-los iguais antes de resolver a operação de adição ou subtração, utilizando as técnicas que a redução de uma fração ao mesmo denominadoroferece.
Para resolver 1/5 + 2/10 é preciso que encontremos o mmc de 5 e 10 (os denominadores diferentes das frações) que será o próprio 10. Encontrando assim as respectivas frações equivalentes 2/10 e 2/10. Com essas frações efetuamos a soma:
2/10 + 2/10 = 4/10, portanto 1/5 + 2/10 = 4/10.
Na operação de subtração o processo é o mesmo, só irá diferenciar-se ao operar.
Comparação de Fração
As frações possuem o objetivo de representar partes de um inteiro através de situações geométricas ou numéricas. Podemos comparar frações utilizando a representação numérica através de algumas técnicas e propriedades. Comparar significa analisar qual representa a maior ou menor quantidade ou se elas são iguais.
1º situação
Quando os denominadores são iguais, basta compararmos somente o valor dos numeradores. Observe a comparação entre as frações ![]() .
.
Note que os denominadores são iguais, dessa forma, vamos comparar os numeradores:
4 > 2 (quatro é maior que dois), então ![]() .
.
Veja outra comparação envolvendo as frações ![]() .
.
Os denominadores também são iguais, assim basta identificarmos qual dos numeradores é maior. Percebemos que 15 é maior que 7 (15 > 7), portanto ![]() .
.
2ª situação
Quando os denominadores são diferentes, devemos realizar operações no intuito dos denominadores se tornarem iguais. Quando eles se tornam iguais aplicamos as definições da 1ª situação. O processo que irá transformar os denominadores em valores iguais é chamado de redução e consiste em descobrir um número pelo qual iremos multiplicar os membros de uma fração para que os denominadores assumam o mesmo valor. Observe:
![]()
As frações dadas possuem denominador 6 e 3, respectivamente. Vamos multiplicar os membros da 1ª equação por 3 e multiplicar os membros da 2ª equação por 6. Veja:
.jpg)
Note que ![]() , portanto
, portanto ![]() .
.
Observe que multiplicamos os membros da 1ª equação pelo denominador da 2ª equação e os membros da 2ª equação pelo denominador da 1ª equação.
Veja mais um exemplo:
Vamos comparar as frações ![]() .
.
Vamos aplicar as reduções nas frações utilizando a regra prática já enunciada.
.jpg)
Observe que ![]() , dessa forma temos que
, dessa forma temos que ![]() .
.
Divisão com frações







.jpg)
.jpg)
.jpg)
.jpg)
.jpg)





.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg) . Elas são formadas por elementos diferentes, mas todas possuem o mesmo valor proporcional. Nesse exemplo, temos que a fração
. Elas são formadas por elementos diferentes, mas todas possuem o mesmo valor proporcional. Nesse exemplo, temos que a fração .jpg)
.jpg)
.jpg)
.jpg)
.jpg)




